TP : Entraîner efficacement mon premier réseau de neurones

Après avoir appris à créer votre premier réseau de neurones dans l’article Mon premier réseau de neurones et avoir étudié la théorie de l’optimisation d’un modèle dans l’article Optimisation simple d’un réseau de neurones, il est maintenant temps de s’exercer à entraîner efficacement un réseau de neurones ! 🚀

Pour cela, nous allons reprendre ensemble la création du modèle de l’article Mon premier réseau de neurones. Nous allons effectuer plusieurs entraînements afin de déterminer l’importance du taux d’apprentissage (learning rate) dans l’entraînement d’un modèle. Si vous avez un doute sur la notion de learning rate, l’article Optimisation simple d’un réseau de neurones est là pour vous accompagner.

Préparation du Notebook

Bien ! Commençons d’abord par toutes les installations et imports dont nous aurons besoin lors de ce TP. Nous utiliserons encore une fois Jupyter pour développer.

On crée un environnement virtuel Python (inutile si vous l’avez déjà créé pour l’article Mon premier réseau de neurones) :

python3 -m venv test_ia

On active l’environnement virtuel Python :

cd test_ia
. bin/activate

On installe Jupyter et on le lance :

pip install jupyter
jupyter notebook

La dernière commande ouvre automatiquement Jupyter dans votre navigateur. Il vous suffit ensuite de créer un Notebook en allant dans « File » → « New » → « Notebook ». Copiez ensuite le code suivant dans le Notebook.

**Installations & Imports ^*1**

^*1 : Cette étape a également été faite dans le premier TP décrit dans l’article Mon premier réseau de neurones.

Il nous faut tout d’abord installer les bibliothèques suivantes :

Pytorch, une des principales bibliothèques Python pour faire des réseaux de neurones. Ici on n’installe que la version CPU, la version de base fonctionne avec CUDA, la bibliothèque de calcul scientifique de Nvidia, mais celle-ci prend beaucoup de place sur le disque dur, restons frugaux.
Pandas, la bibliothèque Python star de la data-science, basée elle-même sur Numpy (pour la gestion de listes).
Matplotlib, pour faire de jolis graphiques.

!pip3 install torch --index-url https://download.pytorch.org/whl/cpu
!pip install pandas
!pip install matplotlib

Une fois les installations effectuées, on peut passer à l’importation de ces bibliothèques ou bien des éléments spécifiques de ces dernières.

import torch
import torch.nn.functional as F

import pandas as pd

import matplotlib.pyplot as plt

from random import randint, seed
# Nous n'avons pas eu besoin d'installer random car c'est une bibliothèque standard de Python

Tout est maintenant en place pour bien débuter le TP !

Création d’un jeu de données

La première étape pour entraîner notre modèle est de créer un jeu de données adapté à notre problématique sur lequel nous pourrons entraîner notre modèle.

On prend cette fois en exemple un skieur en bas d’une montagne qui remonte la pente jusqu’au sommet de cette dernière.

Par conséquent, il nous faut un jeu de données qui représente la pente de cette montagne pour entraîner notre modèle.

Pour cet exemple, on prendra une pente très simple et linéaire d’équation f(x) = 2x. C’est donc cette fonction, une version simplifiée de l’article précédent, que l’on va utiliser pour créer notre jeu de données.

data = pd.DataFrame(columns=["x", "y"],
                    data=[(x, x*2) for x in range(10)],
                   )
data["x"] = data["x"].astype(float)
data["y"] = data["y"].astype(float)

# On peut visualiser le jeu de données d'entraînement ci-dessous
plt.figure(figsize=(25, 5))
plt.margins(0)
plt.scatter(data["x"], data["y"], alpha=0.5)
plt.title("Jeu de données d'entraînement")
plt.xlabel("Position x")
plt.ylabel("Altitude y")
plt.grid(True)
plt.show()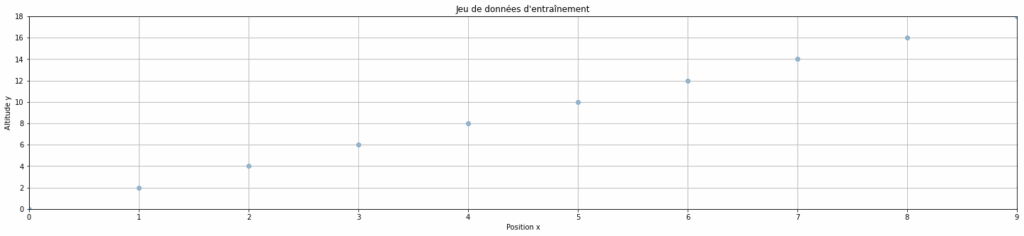

Création de notre modèle

Maintenant que notre jeu de données est prêt, on peut maintenant passer à la création de notre modèle.

On va créer un modèle très simple car notre problématique n’est pas très complexe. En effet, la pente de notre montagne est linéaire, par conséquence, notre modèle n’a besoin que d’une couche de neurones. Pour le créer, on va utiliser PyTotch avec une seed (graine) fixe pour avoir des résultats reproductibles.

torch.manual_seed(1337)
seed(1337)

M = torch.randn((1,1))
M.requires_grad = True

print(M)

Entraînement de notre modèle

Notre modèle ainsi que notre jeu de données étant prêts, on peut maintenant passer à l’entraînement de ce dernier.

Pour entraîner notre modèle, il nous manque encore deux variables à définir : epochs et lr.

epochs (époques) représente le nombre de fois où l’on entraîne le modèle sur un échantillon de données
lr est l’abréviation de learning rate et représente le taux de mise à jour des poids du modèle lors de la descente de gradient (backward pass ou backward propagation)

epochs = 700
lr = 0.1
losses = list()

for epoch in range(epochs):
    # On sélectionne un point de données aléatoire parmi les 10 du dataset
    # Cela permet de varier les données vues à chaque epoch
    ix = randint(0, len(data) - 1)
    x = data.iloc[ix]["x"]
    y = data.iloc[ix]["y"]

    # Forward pass
    y_prevision = M @ torch.tensor([x]).float()

    # Calcul de la loss (perte)
    loss = F.l1_loss(y_prevision, torch.Tensor([y]))

    # Backward pass
    M.grad = None
    loss.backward()

    # Mise à jour du learning rate et de M
    lr = 0.1 # On conserve le même learning rate
    M.data += -lr * M.grad

    # stats : on stocke la loss pour suivre la progression de l'entraînement
    losses.append(loss.item())

Affichage et interprétation des résultats

Lors de l’entraînement, nous avons stocké la loss de chaque epoch, on peut maintenant visualiser comment cette loss a évolué au fil de l’entraînement du modèle.

plt.figure(figsize=(25, 5))
plt.margins(0)
plt.plot(range(epochs), losses, linestyle='-', color='b', label="Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Évolution de la loss au fil des epochs")
plt.legend()
plt.grid(True)
plt.show()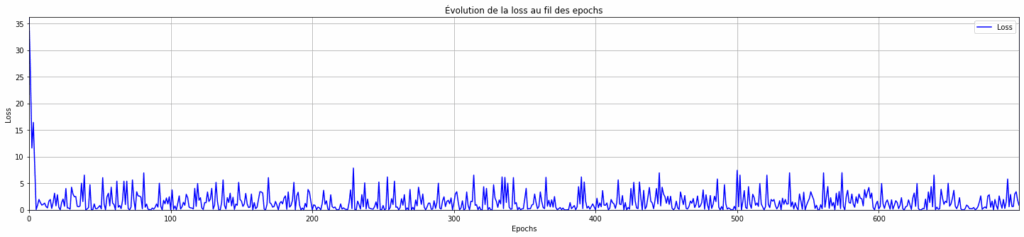

On observe que notre modèle converge très vite, mais à tout de même du mal à se stabiliser (l’ampleur des oscillations reste identique tout au long de l’entraînement).

On peut aussi voir l’impact sur les prédictions des données. En d’autres termes, est-ce que les prédictions sont proches de la pente réelle ? Pour cela, il suffit d’appliquer notre modèle entraîné sur le jeu de données initial.

predictions = []
for x in data["x"]: # Pour chaque x du jeu de données original
    y_pred = (M * x).item() # On applique notre modèle entraîné : y = M * x
    predictions.append((x, y_pred))

plt.figure(figsize=(25, 5))
plt.margins(0)
plt.scatter(data["x"], data["y"], alpha=0.5, label="Données réelles")
plt.plot([x[0] for x in predictions], [y[1] for y in predictions], label="Prédictions", color='r')
plt.title("Données réelles vs Prédictions")
plt.xlabel("Position x")
plt.ylabel("Altitude y")
plt.grid(True)
plt.legend()
plt.show()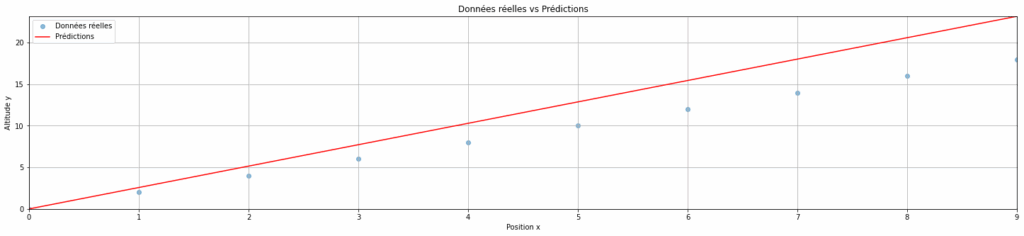

On peut voir que notre modèle fait des prédictions assez proches des données réelles, mais qu’elles ne sont pas tout à fait exactes. Voyons si nous pouvons améliorer notre entraînement.

Entraînement alternatif du modèle

Afin d’améliorer les prédictions de notre modèle, on peut essayer de jouer sur le learning rate.

Pour notre premier test, on a utilisé un learning rate élevé (0,1), ce qui signifie qu’à chaque itération, les paramètres (poids et biais) du modèle sont grandement ajustés (ce qui explique les oscillations sur la loss).

On va donc maintenant tenter le même entraînement, mais avec un learning rate faible (0,001).

torch.manual_seed(1337)
seed(1337)
M = torch.randn((1,1))
M.requires_grad = True
print(M)

epochs = 700 # On conserve le même nombre d'epochs que pour le modèle précédent
lr = 0.001 # On choisit un learning rate plus faible pour voir son impact sur la convergence du modèle
losses = list()

for epoch in range(epochs):
    # Échantillon aléatoire
    ix = randint(0, len(data) - 1)
    x = data.iloc[ix]["x"]
    y = data.iloc[ix]["y"]

    # Forward pass
    y_prevision = M @ torch.tensor([x]).float()

    # Calcul de la loss
    loss = F.l1_loss(y_prevision, torch.Tensor([y]))

    # Backward pass
    M.grad = None
    loss.backward()

    # Mise à jour
    lr = 0.001 # On conserve le learning rate faible
    M.data += -lr * M.grad

    # stats
    losses.append(loss.item())

# Prédictions finales pour les comparer avec les données réelles plus tard
predictions = []
for x in data["x"]:
    y_pred = (M * x).item()
    predictions.append((x, y_pred))

# Visualisation de la loss en fonction des epochs
plt.figure(figsize=(25, 5))
plt.margins(0)
plt.plot(range(epochs), losses, linestyle='-', color='b', label="Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Évolution de la loss au fil des epochs")
plt.legend()
plt.grid(True)
plt.show()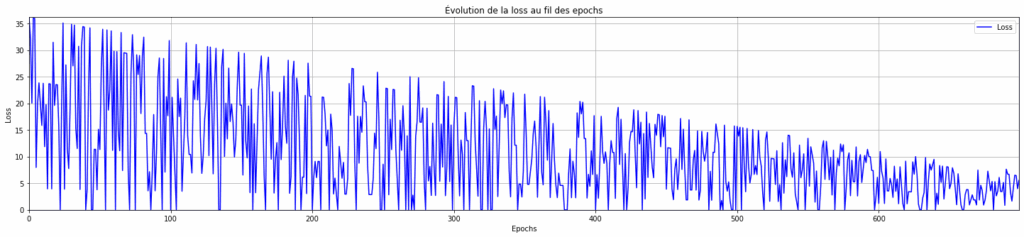

On peut observer qu’avec un learning rate faible, le modèle ne converge pas en 700 epochs (on a toujours une pente descendante et pas de plateau).

Un learning rate faible signifie qu’à chaque itération, les paramètres (poids et biais) du modèle sont très peu modifiés. On essaye de faire des petits ajustements sur ces derniers pour converger avec le moins d’oscillations possibles à la fin de l’entrainement.

Donc, pour converger avec un learning faible, il nous faut un nombre supérieur d’epochs, simplement pour laisser le temps au modèle de converger. Par conséquent, on va retenter l’entraînement précédent, mais cette fois, avec 1000 epochs.

torch.manual_seed(1337)
seed(1337)
M = torch.randn((1,1))
M.requires_grad = True
print(M)

epochs = 1000 # On augmente le nombre d'epochs pour voir si le modèle fini par converger avec un learning rate faible
lr = 0.001 # On conserve le learning rate faible
losses = list()

for epoch in range(epochs):
    # Échantillon aléatoire
    ix = randint(0, len(data) - 1)
    x = data.iloc[ix]["x"]
    y = data.iloc[ix]["y"]

    # Forward pass
    y_prevision = M @ torch.tensor([x]).float()

    # Calcul de la loss
    loss = F.l1_loss(y_prevision, torch.Tensor([y]))

    # Backward pass
    M.grad = None
    loss.backward()

    # Mise à jour
    lr = 0.001
    M.data += -lr * M.grad

    # stats
    losses.append(loss.item())

# Prédictions finales pour les comparer avec les données réelles plus tard
predictions = []
for x in data["x"]:
    y_pred = (M * x).item()
    predictions.append((x, y_pred))

# Visualisation de la loss en fonction des epochs
plt.figure(figsize=(25, 5))
plt.margins(0)
plt.plot(range(epochs), losses, linestyle='-', color='b', label="Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Évolution de la loss au fil des epochs")
plt.legend()
plt.grid(True)
plt.show()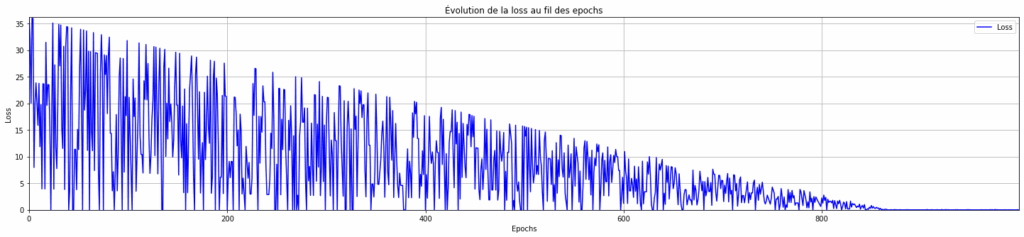

Là, on peut voir qu’avec un learning rate faible (0,001) mais un grand nombre d’epochs (1000), le modèle fini bien par converger.

Mais, est-ce que les prédictions du modèle sont plus justes ? C’est ce que l’on va voir juste après.

plt.figure(figsize=(25, 5))
plt.margins(0)
plt.scatter(data["x"], data["y"], alpha=0.5, label="Données réelles")
plt.plot([x[0] for x in predictions], [y[1] for y in predictions], label="Prédictions", color='r')
plt.title("Données réelles vs Prédictions")
plt.xlabel("Position x")
plt.ylabel("Altitude y")
plt.grid(True)
plt.legend()
plt.show()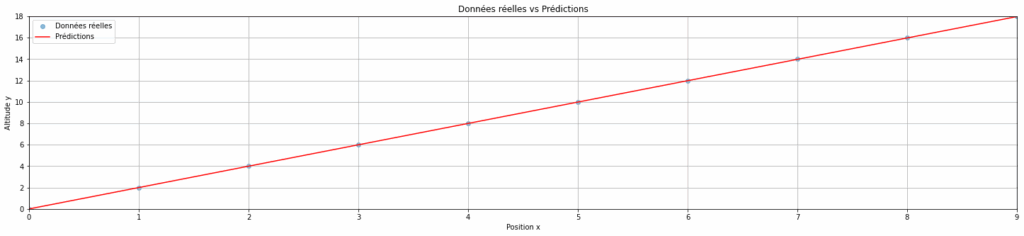

Comme on peut le voir sur le graphique ci-dessus, les prédictions du modèle sont bien meilleures avec un faible learning rate ! 🎉

Entraînement optimale du modèle

Comme vu précédemment, les entraînements avec un learning rate élevé et un learning rate faible ont tous deux leurs avantages et inconvénients.

D’un côté, un learning rate élevé permet au modèle de converger très vite, mais avec de grandes oscillations, ce qui peut, parfois, dire que la loss ne se stabilise jamais et donc le modèle peut faire de mauvaises prédictions. De l’autre côté un learning rate bas permet d’avoir à coup sûr une loss stable à la fin de l’entraînement, mais avec un grand nombre d’epochs, donc un entraînement plus long et un plus grand coût de calculs.

Pour avoir le meilleur des deux mondes, on va tester d’entraîner notre modèle avec un learning rate adaptatif : élevé initialement pour converger rapidement, puis faible pour stabiliser la loss.

torch.manual_seed(1337)
seed(1337)
M = torch.randn((1,1))
M.requires_grad = True
print(M)

epochs = 150 # On repasse à un nombre d'epochs faible
lr_initial = 0.1 # On commence à un learning rate élevé pour converger rapidement
lr_final = 0.001 # On fini à un learning rate faible pour stabiliser la loss
losses = list()

for epoch in range(epochs):
    # Échantillon aléatoire
    ix = randint(0, len(data) - 1)
    x = data.iloc[ix]["x"]
    y = data.iloc[ix]["y"]

    # Forward pass
    y_prevision = M @ torch.tensor([x]).float()

    # Calcul de la loss
    loss = F.l1_loss(y_prevision, torch.Tensor([y]))

    # Backward pass
    M.grad = None
    loss.backward()

    # Mise à jour
    if epoch < 50:
        lr = lr_initial # Pour les 50 premières epochs, on conserve le learning rate initial (élevé : 0,1)
    else:
        lr = lr_final # Passé la barre des 50 premières epochs, on passe à au learning rate final (faible : 0,001)

    M.data += -lr * M.grad

    # stats
    losses.append(loss.item())

# Visualisation de la loss en fonction des epochs
plt.figure(figsize=(25, 5))
plt.margins(0)
plt.plot(range(epochs), losses, linestyle='-', color='b', label="Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Évolution de la loss au fil des epochs")
plt.legend()
plt.grid(True)
plt.show()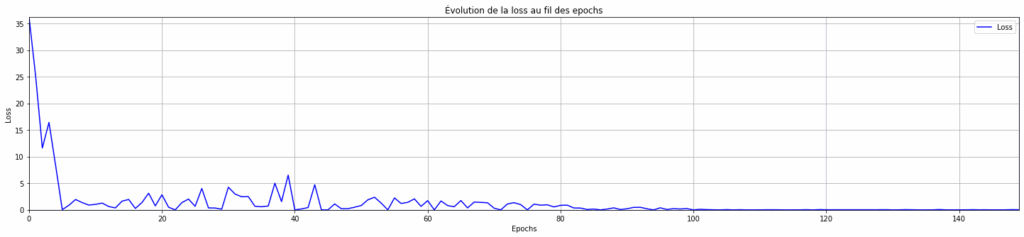

On observe qu’avec un learning rate adaptatif, le modèle converge très bien et la loss se stabilise en un nombre d’epochs très faible !

Donc le learning rate adaptatif est une meilleure solution (en efficacité et performance) pour entraîner un modèle. Le coût d’entraînement est plus faible et le modèle fait de meilleures prédictions.

Cette fonction d’adaptation est en fait appelée un scheduler et elle sert à ajuster dynamiquement un hyperparamètre de l’entraînement. Dans notre cas l’hyperparamètre est le learning rate donc on parle plus précisément de lr scheduler.

Pour notre lr scheduler, nous avons fait une fonction très simple. En effet, on part avec un learning rate élevé, puis, passé 50 epochs, on passe à un learning rate faible.

Cependant, on pourrait également améliorer cette fonction en adaptant notre learning rate en fonction de la dernière loss calculée (et non l’epoch qui est une variable un peu naïve) : tant que la loss diminue on conserve le learning rate actuel, sinon, on le divise par deux. N’hésitez pas à tester cette version de votre côté si cela vous dit !

Conclusion

Pour conclure, dans ce TP, nous avons exploré les notions de learning rate et de scheduler, aspects fondamentaux de l’entraînement d’un réseau de neurones.

Grâce à différents entraînements, nous avons observé que :

✅ La backward pass permet d’ajuster les paramètres d’un modèle en minimisant une fonction de loss.

✅ Le choix du learning rate est crucial : trop élevé, la loss est instable ; trop faible, elle devient trop lente.

✅ Un learning rate adaptatif permet d’accélérer la convergence au début et de stabiliser l’apprentissage ensuite.

✅ Il existe plusieurs façons d’adapter le learning rate et les fonctions d’adaptation de ce dernier sont appelées des schedulers.

N’hésitez pas à prendre en main ce TP de votre côté pour bien maîtriser la création et l’entraînement d’un réseau de neurones. Vous pouvez par exemple tester différents learning rate ou lr schedulers pour l’entraînement de votre modèle ! 🚀

Auteur : Mathilde POMMIER, Neogeo

TP : Entraîner efficacement mon premier réseau de neurones

Préparation du Notebook

**Installations & Imports ^*1**

Création d’un jeu de données

Création de notre modèle

Entraînement de notre modèle

Affichage et interprétation des résultats

Entraînement alternatif du modèle

Entraînement optimale du modèle

Conclusion

admin

Previous PostRenouvellement de la plateforme GéoJura pour le SIDEC

Next PostVotre chatbot OneGeo Chat : décryptage technique

TP : Entraîner efficacement mon premier réseau de neurones

Préparation du Notebook

Installations & Imports *1

Création d’un jeu de données

Création de notre modèle

Entraînement de notre modèle

Affichage et interprétation des résultats

Entraînement alternatif du modèle

Entraînement optimale du modèle

Conclusion

admin

Previous PostRenouvellement de la plateforme GéoJura pour le SIDEC

Next PostVotre chatbot OneGeo Chat : décryptage technique

**Installations & Imports ^*1**